Solution:

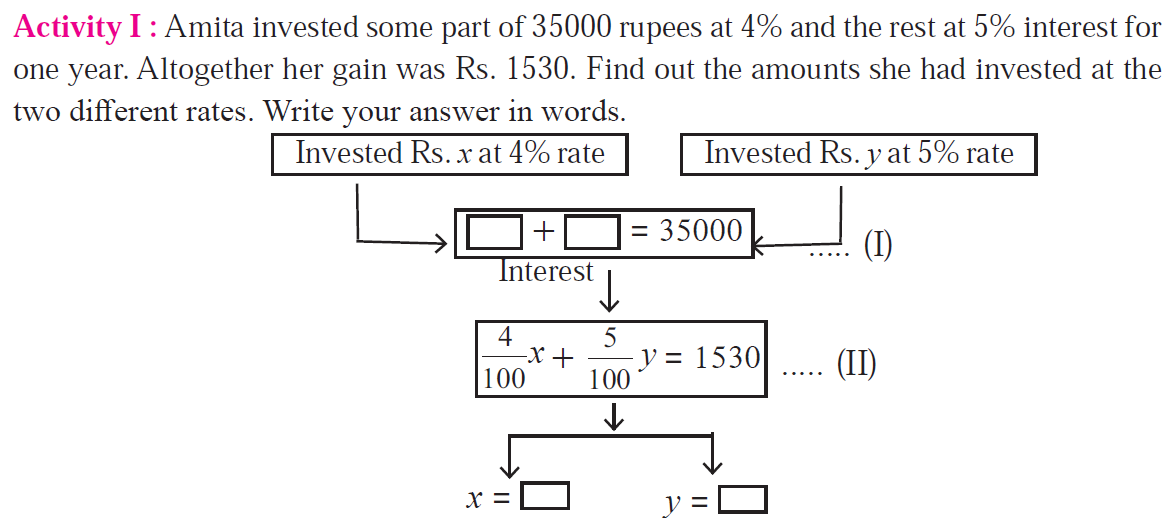
Let the amount invested at 4% be x and the amount invested at 5% be y.

From the given information, we have:

\(\displaystyle x + y = 35000\) ... (I)

And

\(\displaystyle \frac{4}{100}x + \frac{5}{100}y = 1530\) ... (II)

∴ \(\displaystyle \frac{4x + 5y}{100} = 1530\)

∴ \(\displaystyle 4x + 5y = 1530 \times 100\)

∴ \(\displaystyle 4x + 5y = 153000\)... (III)

Multiplying (I) by 4:

\(\displaystyle 4x + 4y = 140000\) ... (IV)

Subtracting (IV) from (III):

		4x	+	5y	=		153000	... (III)
−	㊉	4x	㊉	4y	=	㊉	140000	... (IV)
	−		−			−
				y	=		13000

∴ \(\displaystyle y = 13000\) ... (V)

Substituting the value of y in (I):

\(\displaystyle x + 13000 = 35000\)

∴ \(\displaystyle x = 35000 - 13000\)

∴ \(\displaystyle x = 22000\) ... (VI)

∴ Amita invested ₹ 22,000 at the rate of 4% and ₹ 13,000 at the rate of 5%.